13 November 2010
Natural Hazards and UnNatural Disasters – the Economics of Effective Prevention
Posted by Dave Petley
This week a joint publication was released by the United Nations and the World Bank with the above title. The aim of the report, which can be downloaded for free from here, was to exemine the efficacy of investment in disaster risk reduction. Although long, it is an excellent piece of work that is inevitably destined to be influential in this area. As usual with reports associated with the World Bank, which tend to follow a particular economic model for development in less developed countries that has proven to be less than effective in many locations in my view, there are aspects with which I disagree. However, the key points are generally worthy and thought-provoking. As an aside it has been interesting, and slightly depressing to see how little traction this report has gained in the mainstream media. Given the high profile disasters of the last few years this is disappointing.
For me the most important aspect of this report is the justification that it provides for investment in disaster risk reduction. Superficially, one might think that this is an obvious course of action, but an alternative argument can be, and sometimes is, articulated. The table below compares the number of people killed per annum by various issues around the world:
- Natural Disasters : 80,000 (EM-DAT based on 2005-2009)
- HIV-AIDS: 2 million (UN based on 2008)
- Malaria: 880,000 (WHO based on 2006)
- Water quality: 2.2 to 5 million (Gleick 2002)
- Maternal deaths in childbirth: 358,000 (UNICEF based on 2008)
In this context, the argument is that the (scandalously) limited sums available for investment in development aid are better targetted at these other issues, and that disaster risk reduction can follow on in due course. Of course, that is completely incorrect, and this report cogently explains why. The key reasons are as follows:
1. Investment in disaster risk reduction saves money in the long term
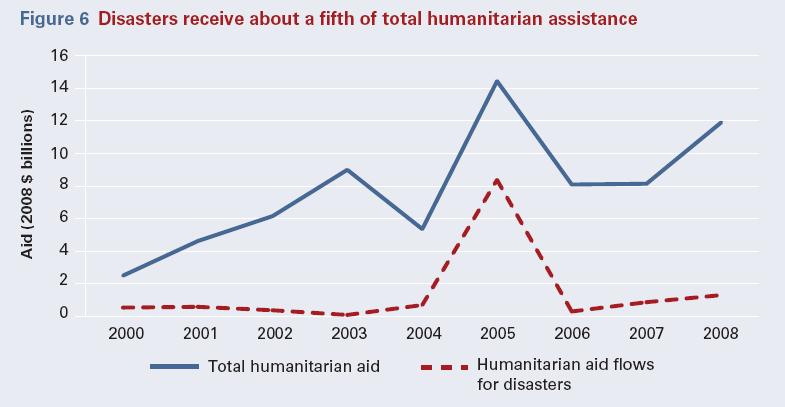
The report points out that disaster risk reduction is cost-effective because it is generally much cheaper to mitigate hazards than it is to deal with their aftermath. Whilst this is neither new nor surprising, the report contains a fascinating graph that demonstrates that disaster relief accounts for about one fifth of the humanitarian budget on an annual basis:
2. Disaster risk reduction does not need to be expensive
In many cases investment in disaster risk reduction does not need to compete with other demands on resources simply because the costs are often low and can be widely distributed. Thus, for example, the cost of building in seismic-resistant design elements to building under construction are low in comparison with the overall expense, and can ensure not only safety of the occupants but also of the investment in the building.
The report makes the point that the costs of disasters are likely to rise dramatically for two reasons. The first is climate change. I know that this will promote howls of protest from the “sceptic” community, but the geohazard / geophysical and disaster reduction communities, who work on these issue on a daily basis, are like me in no doubt, and speak from a well-informed position, so I do not intend to discuss this further here. Climate change is expected to increase the occurrence of the most damaging storm events, with congruent increases in resulting losses. Secondly, the growth of cities vulnerable to major natural hazards is alarming – by 2050 it is expected that 1.5 billion people will live in cities vulnerable to earthquakes and tropical cyclones.
So, the report has four main findings:
- Disasters expose the cumulative implications of many earlier decisions. The report advocates a deeper investigation in the aftermath of disasters into why particular decisions were taken. The idea here is not recrimination but lesson learning.
- Prevention is possible and often cost-effective, as described above.
- Many measures – both public and private – must work together for effective prevention. The use of prevention is a little odd here, but the theme is actually mitigation and preparation, the point being that a lack of joined up thinking can result in unintended consequences. This in part explains the prevalence of disasters in less developed countries. Weak and immature governments rarely make good, coherent decisions, with terrible consequences;
- The exposure to hazards will rise in cities, but greater exposure need not increase vulnerability. The point here is that the growth of vulnerable cities appears inevitable, but that appropriate planning and mitigation can prevent a consequent increase in disasters.
Thus, the report makes five recommendations for policy:
- Governments can and should make information more easily available. I agree with this wholeheartedly, but would want to emphasise that in many cases the issue is not data availability but rather the capacity of potentially-affected people to use the information in an effective way. This issue, which occurs in every society, needs further thought;
- Governments should permit land and housing markets to work, supplementing them with targeted interventions when appropriate. This sounds worryingly like the World Bank’s dogma on the joy of free markets and is, I think, rather unconvincing in all but a few cases. I am not arguing against free markets, but rather that their benefits are somewhat overstated;
- Governments must provide adequate infrastructure and other public services. The report makes the point that often investment in public infrastructure is essentially irrational due to political considerations. Interestingly, the report points out that investment in rural roads is particularly problematic – this is a hobby-horse that I frequently ride.
- Good institutions must develop to permit public oversight. They use the example of deforestation in Haiti – the subject of a post a couple of days ago – to point out the need for good institutional structures.
- Donors have a role in prevention. The report notes that spending on prevention is less than one per cent of the total aid budget, but as noted above response to disasters consumes about a fifth of it. This suggests that much more investment is needed in prevention.






 Dave Petley is the Vice-Chancellor of the University of Hull in the United Kingdom. His blog provides commentary and analysis of landslide events occurring worldwide, including the landslides themselves, latest research, and conferences and meetings.
Dave Petley is the Vice-Chancellor of the University of Hull in the United Kingdom. His blog provides commentary and analysis of landslide events occurring worldwide, including the landslides themselves, latest research, and conferences and meetings.
[…] & Fire Damage Restoration Equipment Floods are the most frequent natural hazard in Canada. They can occur at any time of the year and ar… href="http://www.hc-sc.gc.ca/index-eng.php" target="_blank">Health Canada has numerous […]