3 November 2010
Updates – the Canterbury earthquake railway line; Hurricane Tomas and Haiti; and Manchhar lake in Pakistan
Posted by Dave Petley
This is a general update email on a range of recent posts:
 1. The railway line affected by the Canterbury Earthquake in New Zealand
1. The railway line affected by the Canterbury Earthquake in New Zealand
Yesterday I posted the image to the left of the deformation to a railway line were it crossed the surface expression of the fault that was responsible for the Canterbury Earthquake in New Zealand. A number of people contributed to the discussion (thanks to you all) – the general consensus was that it is indeed a compressional feature associated with a broad zone of deformation rather than a distinct shear plane. I was emailed by Steve Hill, an engineer, who offered the following explanation (reproduced here):
First, some points about the railway line:
– It is VERY rigid in the vertical axis, not so much in the horizontal. This is so that it can carry load and distribute it over a large number of crossties, yet be bent around a curve without major bending machinery (basically, it can be bent around even tight radius turns with little more than large levers).
– The crossties pin the rails a fixed and uniform distance apart
– In the picture, there is no vertical deformation (see point one) or any rotation of the track assembly.
– This deformation occurred along a VERY straight line of track
– You will note that none of the fasteners that join the rail to the cross-ties have failed.
– If you look at the first picture (the one with the motive power in it) and compare it to the second, you will note that the entire failure is VERY symmetrical.
From here it’s simple geometry: the failure is symmetrical, and failed in both directions at the same time, because geometry requires it. The rails failed in their weakest axis, and since, over the failure zone they are of equal length, geometry dictates that as long as they maintain their uniform separation, the rails MUST maintain the same distance (length) over the failure zone. If one labels the ends of the failure as (arbitrarily) Points A and B, then the two rails, pinned an unchanging distance apart between those two points, MUST maintain their length between those two points. Since that length is equal, they must spend equal amounts of length on the inside and outside of any common radii they share – thus the symmetrically of the failure. This can be seen when one extends an imaginary line from the vanishing point of the photo, down the center of the track assembly. You will note that the rails are displace (roughly) equally on either side of that imaginary line, again, because geometry dictates that they must. Another bit of evidence of this is that if one looks closely, one will note that NONE of the ties have rotated – they have all displaced laterally.
Very interesting. Comments?
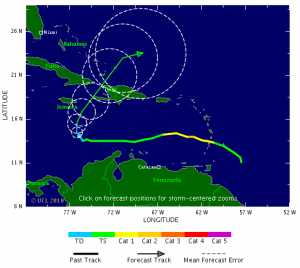
The good news is that Hurricane Tomas has weakened in the last 24 hours, and is now technically a tropical depression. The bad news is that it has now started its turn to the north, which increases the chances that the storm will pass close to the earthquake affected areas of Haiti. Tropical Storm Risk has produced the track map shown to the left. The current forecast suggests that it will pass close to Haiti in about 48 hours from now. At that point it is forecast to have strengthened again. Based on the current trajectory (and note that there are huge errors in forecast tracks), the intense rainfall associated with the storm will be a substantial hazard to the displaced population. The forecast slow rate of movement of the storm is good from a winds perspective, but very bad with respect to rainfall. This situation remains deeply troubling, but no particular outcome is likely at this point.
3. Manchhar Lake in Pakistan
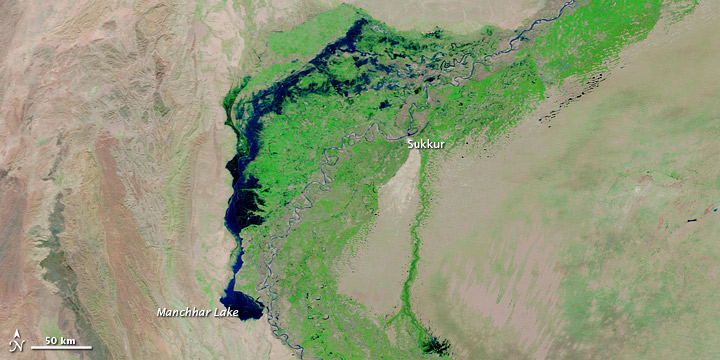
The floods in Pakistan, which I have covered extensively over the last few months on this blog, have now faded from the headlines, but amazingly the water has yet to retreat fully. NASA have a new satellite image on their website showing the extent of the water in the southern part of the country:
Note the main Indus channel to centre and the east of the image, and the huge flooded area to the west. Manchhar Lake itself remains at a hugely elevated level, but the really notable impact is the vast flooded area to the north of this. Note the scale bar on the lower left of the image – this water is covering a vast area. Of course the implication of this is that a large number of people remain displaced and, increasingly, malaria is a serious threat. What is not clear from this image is whether water is still flowing into this area at the north end of the image. If so then in effect the river has reoccupied a old channel system.


 Dave Petley is the Vice-Chancellor of the University of Hull in the United Kingdom. His blog provides commentary and analysis of landslide events occurring worldwide, including the landslides themselves, latest research, and conferences and meetings.
Dave Petley is the Vice-Chancellor of the University of Hull in the United Kingdom. His blog provides commentary and analysis of landslide events occurring worldwide, including the landslides themselves, latest research, and conferences and meetings.
MSNBC has photos of landslides in Costa Rica
http://www.msnbc.msn.com/id/40009265/ns/weather/
“SAN ANTONIO DE ESCAZU, Costa Rica — A rain-sodden hillside collapsed on homes in a suburb of Costa Rica’s capital, killing at least 20 people and leaving several dozen missing, officials said Thursday as landslides and flooding across the nation led to a “red alert” declaration.”