2 March 2011
Geologic models
Posted by Jessica Ball
I will admit to shamelessly stealing the subject of this post from a Fluid Dynamics in Volcanology class that I’m taking right now. (My brain pretty much screamed “blog post” mid-discussion today, and as I have no other topics in mind, this will do.)
The discussion was about the different kinds of models we use in geology, and how we make sure they’re useful. The main categories that we discussed were conceptual models, mathematical models, experimental models, and geologic maps. (I’ll hit the maps part of it later on; rest assured that there is a good reason for calling a map a model.) The goal of a model is to distill the basic principles of geologic phenomena into a simplified version of what you’re trying to explain. For example, no one can tell exactly where every single particle of ash in a volcanic plume will go, but with models of plume behavior, we can get an idea of how the plume as a whole will behave, and where the majority of those particles will end up.
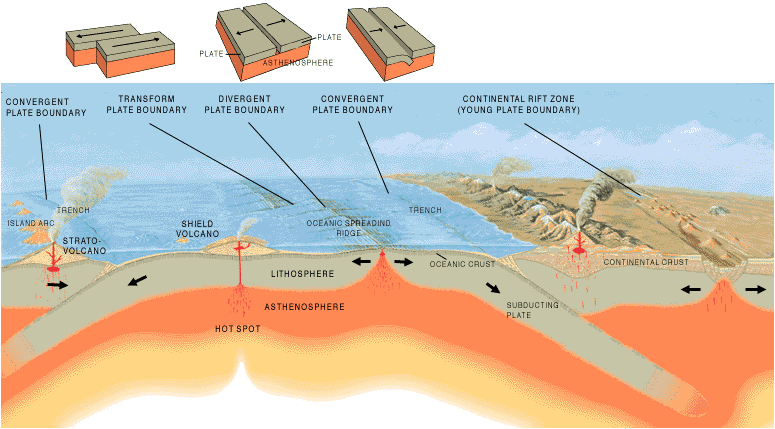
Artist's cross section illustrating the main types of plate boundaries (Cross section by José F. Vigil from This Dynamic Planet - USGS/Smithsonian Institution/U.S. Naval Research Laboratory)
Conceptual models are verbal or written (or drawn) descriptions of how a geologic process works. Geologists use these a lot, especially when we can’t actually go out and point to what we’re describing. An excellent example would be the cross-sections of different types of plate boundaries; these are simplified depictions of what goes on in a subduction or collision zone, or at a hot spot, or at a transform fault. This kind of diagram can’t possibly show you things like the formation of fault gouge, or slab detachment, or the effects of upwelling magma on seismic wave velocities. It’s not meant to recreate exactly what’s going on, but rather to give you a general idea of the major processes at work.
Mathematical models rely on some knowledge of physics – mainly an ability to describe physical processes in mathematical terms. Geologists use mathematical models a lot – to describe everything from hillslope erosion to groundwater in an aquifer to the internal structure of the Earth. In the class I’m currently taking, we spend quite a bit of time looking at fluid dynamics-based models of volcanic phenomena – things like the spreading of eruption plumes, the paths of ballistics in explosive eruptions, the formation and growth of bubbles in magma, and the movement of pyroclastic flows. In fact, the University at Buffalo has a fairly new website called VHub, which is a repository of simulation tools based on many of these models of volcanic phenomena. (It’s also free to join, and you can use the tools online rather than working with the original code – VHub is meant to make them easily and immediately available for hazard mitigation purposes.)
Experimental models are physically doing something in the lab or the field – usually a small-scale version of a geologic process that you can’t initiate or observe closely in nature for various reasons (often safety-related). This is, in my opinion, one of the most fun (funnest?) parts of being a geologist. These can be as simple as the mentos-and-diet-soda “eruptions” or something as complicated as creating artificial eruption plumes and pyroclastic flows. One of my particular favorites is the Cascade Volcano Observatory’s Experimental Debris-Flow Flume, where CVO scientists constructed an inclined ramp that they can dump material down in order to create debris flows in a controlled situation. (The videos of these experiments are especially cool – take a look if you have time!)

A portion of the geologic map of Grand Canyon National Park, USGS Geology Of The National Parks website
Geological maps are simplified versions of the surficial geology in an area. It’s impossible to map something in so much detail that you know exactly where every boulder, fracture, and contact is, no matter how good your imagery is or how long you spend in the field. Therefore a map must be a simplification of what’s actually going on; a cross-section is even more so, because there’s no such thing as a quad-wide roadcut to the depths that most cross-sections extrapolate to. Instead, we make the most detailed observations we can, draw interpretations from them, and distill that information down into a neat collection of lines and colors. (Anyone who’s ever done geologic mapping knows that geology on the ground certainly doesn’t look that nice!)
In models (especially experimental and mathematical ones), it’s impossible to account for every single variable that might affect the process(es) in question. Ideally, simplifications are made based on what factors can be reasonably discarded because their effects are negligible or unimportant to the question you want to answer with the model; in real life, simplifications are often made because trying to include everything would make the model impossibly complicated.
One part of the discussion talked about the differences between a model and a simulation. The two words are often used interchangeably, but in this class the professor chose to separate them by their ultimate purpose and result. The most basic way to distinguish the two might be this: a model describes, while a simulation predicts. For example, weather forecasting uses models – mathematical and otherwise – to describe the conditions under which certain weather types will occur, but then runs simulations based on these models (and known data) to predict weather behavior for the next few days.
Finally, we talked about what makes a good model – and how you know it’s a good model before you start doing things like dumping a few tons of rock down a hill. The qualifications we discussed are that the model must have geometric similarity and dynamic similarity to the geological phenomenon it’s describing. To have geometric similarity, a model must look the same as the natural system – as in, the proportions of the model should match those of the natural setting. (Basically, if you have a stream channel that’s 100 m wide and 1 m deep, your model of the channel should not be 1 meter wide and half a meter deep – it should be 1 m wide and 1 cm deep.) Some allowances are necessary for things like model boundaries – if you’re using a tank of fluid to model a volcanic plume rising through the atmosphere, your tank does not have to be anywhere near as big as the Earth’s atmosphere . At some point, the boundaries of the experimental setup will have only negligible effects on the experiment, so you can keep things to a little smaller scale. To have dynamic similarity, the same (or analagous) processes must be the dominant controls on the phenomenon’s behavior in both systems. (In other words, you can’t use a garden hose to provide water for hillslope erosion if you’re trying to model the effects of rain. Both involve adding water to the system, but a stream of water water from a hose is closer to the processes that occur in a flood than what goes on when rain falls.)
Geology is a great science in that it uses so many different models to help us understand our subject matter, and combines groundwork as well as mental gymnastics to help formulate them. One of the things I enjoy about graduate school is that you get the chance to start using the more complicated models – and maybe even develop some yourself!



 Jessica Ball is a volcanologist at the U.S. Geological Survey, researching volcanic hydrothermal systems and stability, and doing science communication for the California Volcano Observatory. She previously worked at the Geological Society of America's Washington DC Policy Office, learning about the intersection of Earth science and legislative affairs. Her Mendenhall postdoc and PhD focused on how water affects the stability of volcanoes, and involved both field investigations and numerical modeling applications. Her blogging covers a range of topics, from her experiences in academic geosciences to science outreach and communication to her field and lab work in volcanology.
Jessica Ball is a volcanologist at the U.S. Geological Survey, researching volcanic hydrothermal systems and stability, and doing science communication for the California Volcano Observatory. She previously worked at the Geological Society of America's Washington DC Policy Office, learning about the intersection of Earth science and legislative affairs. Her Mendenhall postdoc and PhD focused on how water affects the stability of volcanoes, and involved both field investigations and numerical modeling applications. Her blogging covers a range of topics, from her experiences in academic geosciences to science outreach and communication to her field and lab work in volcanology.
We use conceptual ore deposit models in mineral exploration; these are often written and range from simple and able to fit on a 5×8 card to complex and detailed, with diagrams, and taking up several pages. Models are not always agreed upon through the industry, and people inventing, discovering, or creating new models that lead to discovery of ore deposits have been known to be quite successful.
Hi,
interesting article.
At the British Geological Survey we are in the middle of transferring our entire business process from “maps to models”. http://www.bgs.ac.uk/science/3Dmodelling/mapstomodels.html
Therefore the boundaries between the definitions of different models are becoming blurred. Our aim is to convert all geological maps into 3D geological framework models that will serve as both conceptual models and a database for numerical modellers.
Some more information is published here: http://www.bgs.ac.uk/research/CCP/DREAM.html and the methodology we are using to create geological models is available here http://www.gsi3d.org.uk
Wow – that’s a wonderful way of combining models! I’ll definitely have to take a look, and maybe turn this into a followup post. Thanks for bringing it to my attention!