14 April 2010
Using bedding / cleavage to detect overturned beds
Posted by Callan Bentley
One of my students wrote to me this morning with a question about the relationship between bedding, cleavage, and folding. He asked:
I am not sure how we use the relationship between bedding and cleavage to interpret fold limbs. It seems if bedding is near vertical and cleavage is closer to horizontal, this would be an upright fold limb. To be overturned, wouldn’t the bedding need to be closer to horizontal? I guess I don’t understand how does cleavage help dictate the bedding orientation.
So here’s the deal: when rock strata (layers) get compressed, they develop a couple types of structures: one is that they tend to fold, and the other is that they tend to cleave. Cleavage and folding have a distinctive relationship. Say bedding starts off horizontally-oriented, and is subjected to a horizontal compressive stress. Cleavage will form that is vertically-oriented (perpendicular to σ1). As deformation proceeds and the bed begins to shorten by buckling up and down, the cleavage “tips” over (rotates) as the top of the bed moves towards the fold crest. (I have previously discussed a similar aspect of vergence, using S and Z folds. The same thing that applies to the axial planes of parasitic folds also applies to cleavage.)
Assuming a simple single episode of deformation (no overprinting), the orientation of the cleavage plane will be approximately the same as the axial plane of the main fold (an imaginary geometrical plane that “divides a fold into left and right halves”).
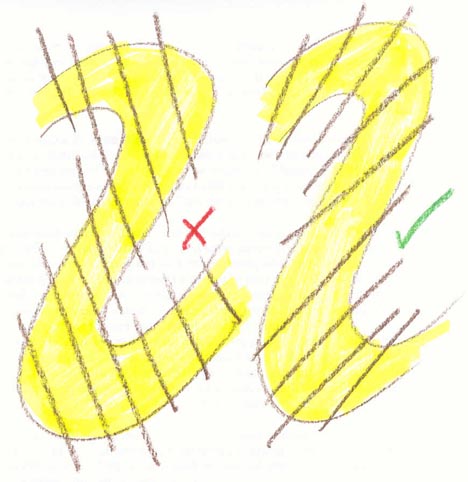
Here’s a quick sketch I just drew of a folded bed (yellow) being cut by cleavage (parallel brown lines):
In the example on the right, the cleavage and folding agree with one another (that is, the folds’ axial planes and the cleavage planes are parallel): one episode of compression could produce these two structures in these orientations. In the example on the left, the cleavage cuts across the fold at an angle which is close to orthogonal (perpendicular) to the axial plane of the folds — this is an impossible situation to produce with a single episode of deformation.
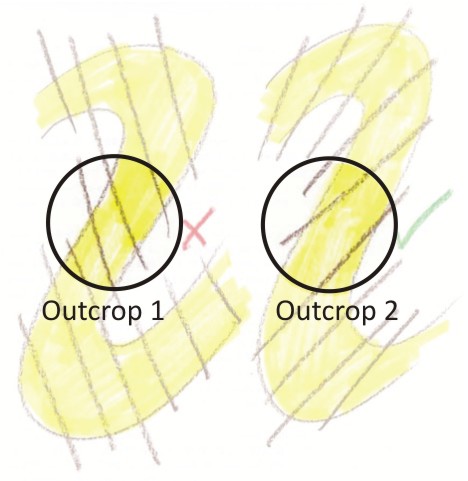
If you were to find an outcrop of the yellow layer (circular zones of exposed rock in the diagram below) that showed the relationship between the cleavage and the bedding, you can interpret the overall structure:
Outcrop 1 shows bedding and cleavage dipping in opposite directions. Outcrop 2 shows bedding and cleavage dipping in the same direction, though bedding is dipping more steeply than cleavage.
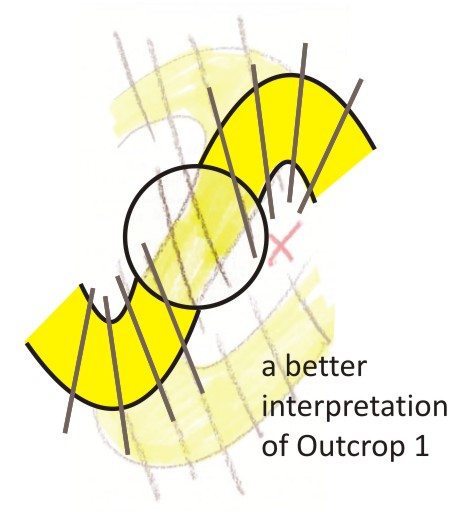
Because of this relationship, Outcrop 2 is best interpreted as an overturned limb of a fold. But Outcrop 1 doesn’t make any sense as it is drawn above. The best way to interpret that circular exposure is shown here:
…That is: it is an upright limb of a fold, not an overturned limb.
So: if you have a steeply-dipping bed cut by more-shallowly-dipping cleavage, pay attention to the direction of the cleavage’s dip: (a) If it is dipping in the opposite direction as bedding, your fold is upright or asymmetric. (b) If your bedding and cleavage are dipping in the same direction, your fold is overturned. If the bedding and cleavage are both close to horizontal (and part of a larger fold), then you’ve likely got the limb of a recumbent fold. If bedding is vertical and cleavage is horizontal, you’re likely on the nose of a recumbent fold, where the axial plane cleavage is intersection bedding at a right angle. If bedding is horizontal but cleavage is vertical, then the deformation likely hasn’t proceeded very far. Obviously, checking for geopetal structures like cross-bedding or mudcracks can help you determine whether the beds are overturned or not from a purely sedimentological point of view.
Hopefully this post helps elucidate the structural relationship between bedding and cleavage a bit more. If not, read here about a classic example in Wisconsin (Van Hise Rock).


 Callan Bentley is Associate Professor of Geology at Piedmont Virginia Community College in Charlottesville, Virginia. He is a Fellow of the Geological Society of America. For his work on this blog, the National Association of Geoscience Teachers recognized him with the James Shea Award. He has also won the Outstanding Faculty Award from the State Council on Higher Education in Virginia, and the Biggs Award for Excellence in Geoscience Teaching from the Geoscience Education Division of the Geological Society of America. In previous years, Callan served as a contributing editor at EARTH magazine, President of the Geological Society of Washington and President the Geo2YC division of NAGT.
Callan Bentley is Associate Professor of Geology at Piedmont Virginia Community College in Charlottesville, Virginia. He is a Fellow of the Geological Society of America. For his work on this blog, the National Association of Geoscience Teachers recognized him with the James Shea Award. He has also won the Outstanding Faculty Award from the State Council on Higher Education in Virginia, and the Biggs Award for Excellence in Geoscience Teaching from the Geoscience Education Division of the Geological Society of America. In previous years, Callan served as a contributing editor at EARTH magazine, President of the Geological Society of Washington and President the Geo2YC division of NAGT.
I’m an Auburn student currently studying for a Structural final and you have no idea how much this helped! Great explanation and pictures! Saved me a huge headache, thanks from me and the countless people from my class I’m going to have to explain this to now!
[…] then I could share it with the entire class: more learning return on my instructional investment! I wrote up the post, put it online, and e-mailed the link to my whole class. […]
Dear Sir,
Very nice discussion.
Is there any relationship of Cleavage and faulting?
Regards,
Haroon
“Is” there? Probably somewhere, but not here…
🙂
Oh lets find out where is it..:P. Actually i was thinking, as we know there is relationships among most of the structural features with each other, if you find any regarding my question, please post on your blog.
Thnx
Regards
Syed Haroon Ali
[…] over. Imagine that we rotated these strata clockwise by 30°. Then they would be overturned, and the cleavage and bedding would be dipping in the same direction, though the bedding would be more steeply tilted than the […]
[…] a roadside explanation just an hour and a half earlier on how the relationship between bedding and cleavage can reveal whether bedding is likely right-side-up or up-side-down, my students and I were walking up the road to the Ancient Bristlecone Pine Forest in the White […]
[…] You know what that means: These beds must be overturned! […]
What an explanation sir..loved it
I am A Student from India and presently preparing for my Doctoral Entrance. I was stuck at this concept for days because I could not visualize the scenario. Your explanation have cleared all doubts and hammered the concept into my head. It was great help. Looking forward to coming across more of your expanations. Cheers!! 🙂
This is such a great and informative explanation. Helped a lot as I was studying for my structure final
Thank you
This is so perfect!
[…] One of my favorite tricks is using bedding / cleavage intersections to identify tectonically inverted strata. […]