5 March 2010
Is this dike a feeder?
Posted by Callan Bentley
A new paper in the journal Geology examines an interesting question: how can you tell feeder dikes from non-feeder dikes?
The answer is, normally you can’t. Normally, there’s no way to tell for sure whether a given dike actually funneled magma to the paleo-surface, or whether it never reached the paleo-surface. The reason for this is that usually, the paleo-surface is gone by the time the dike is exposed at the modern surface to your scrutiny. In the new paper, a team of Japanese researchers examined the plumbing of Miyakejima Volcano, which collapsed during an eruption in the year 2000. The collapse opened up a view into the volcano’s “guts,” which showed the anatomical details of many dikes.
Here’s Figure 2B from the paper (reproduced, as with Figure 3 below, with permission of the publishers of Geology), showing the extraordinary exposures on this volcano. The authors report that they were able to trace an individual dike for more than 350 meters. In this example, you can follow a feeder dike up 150 m to find where it erupted at the paleosurface in a cinder cone!
So, given such an extraordinary exposure, how do you go about assessing the geometries of the dikes? The research team used photography as their tool. Hopefully it will be obvious that examining the dikes in person would be difficult and dangerous on a subvertical cliff many hundreds of meters tall — and on an unstable and crumbly volcano, to boot! So they took photos, and then did their measurements based on the photos. They claim a resolution of about 3 cm per pixel at a distance of about 1 km.
Filtering your data through a medium like photography is a good way to introduce error and bias to your study, and the authors took some steps to avoid that. They used good zoom lenses, aimed at the outcrop face from the safety of the opposite side of the caldera, and aimed them straight on to the dike outcrops (i.e., within 10° of the strike of the dikes, not necessarily orthogonal to the cliff face, since there is no guarantee the dike would intersect the cliff face at a right angle): so the apparent thickness was as close as reasonably possible to the true thickness. For each photo, they cut off a 20% margins on each side of the image (total cropped area: -40%), as a guard against the effects of lens distortion. Finally, they double-checked their accuracy by comparing in-person measurements of objects of known size on the caldera rim to their photo-measurements of those same objects.
They defined feeder dikes as those (as in the image above) which were observed to connect directly to the bottoms of spatter cones and diatremes. They defined non-feeder dikes as those which terminated “either by tapering away inside layers or ending bluntly at layer contacts,” where the ‘layers’ being referred to are pyroclastics and lava flows within this stratovolcano. In total, they tallied up 165 dikes, 93% of which were “non-feeders.” Of these, they selected the 27 best-exposed (21 non-feeders and 6 feeders) for their analysis.
What did they find? To quote from their abstract:
A typical feeder thickness reaches a maximum of 2–4 m at the surface, decreases rapidly to ~1 m at a depth of 20–40 m, and then remains constant to the bottom of the exposure. By contrast, a typical non-feeder thickness reaches a maximum of 1.5–2 m at 15–45 m below the tip, and then decreases slowly with depth to 0.5–1 m at the bottom of the exposure.
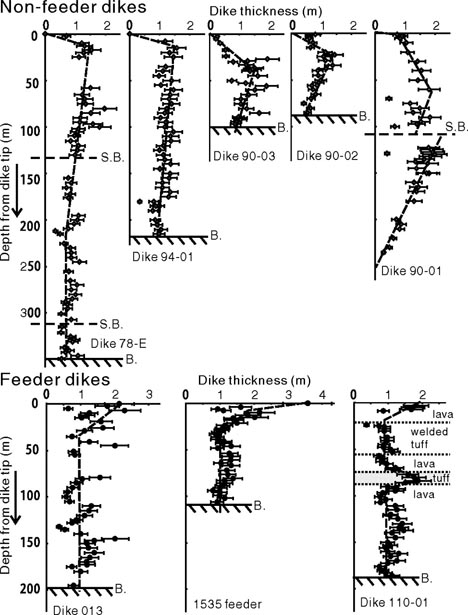
Width vs. depth data from five representative non-feeder dikes are plotted in their Figure 3, top row, and three representative feeder dikes in the second row of Figure 3. Check it out:
Feeder dikes open up (get wider) at the surface, but the non-feeder dikes first get wider (gradually positive trend to these plots), and then abruptly pinch out up towards the tip (sudden leftward cant at the top of the plot). The authors ponder these dramatically different profiles, and offer an explanation.
They offer two equations which describe these dike profiles pretty accurately. If you’re not mathematically inclined, take a deep breath. We’ll translate in a few column-inches! The first equation is:
b = (2Po(1-v2)L)/E
where b is the thickness of the dike, Po is the magmatic overpressure (the pressure in excess of the normal stress on the dike at the point of measurement), v is Poisson’s ratio, a measure of how much volume is conserved during strain for the host rock. In other words, when a material is compressed in one direction, how much do the other directions pooch outward? Call it ‘poochiness.’ E is Young’s modulus, a measure of the elasticity of the host rock. L is the “dike-controlling dimension,” that is whichever of the dimensions of the dike (either the dip-dimension or the strike-dimension) is smaller. So, to translate this equation into “English” enough that even Rick Sanchez could understand it, equation #1 says, ” The thickness of a dike of a given height depends on how much pressure the magma opening and filling the dike is under, along with how ‘poochy’ and elastic the host rock is.”
The second equation is:
Po = (ρr–ρm)gh + ρc + σd
where ρr is the density of the host rock, ρm is the density of the magma, and g is the acceleration due to gravity. The variable h is the dip dimension (height) of the dike (measured upward from the source magma chamber), ρc is the excess magmatic pressure in the source chamber before rupture (dike injection), and σd is the difference between the maximum and minimum principal stresses. Let’s translate this one, too: “The pressure exerted by the magma filling a growing dike depends on the difference between the density of the magma and the host rock it’s intruding into, as well as the force exerted on the magma by gravity. Another important factor is whether there are significant tectonic stresses impinging on the dike as it forms.”
So where does that leave us in interpreting Figure 3, showing those different profiles for feeder dikes versus non-feeder dikes? Equation #2 says that the magmatic overpressure in a dike (Po) will increase as the dike propagates upwards (gets taller, in other words: h goes up). And equation #1 says, if the magmatic overpressure increases, then the dike will get thicker. That’s why the non-feeder dikes get thicker and thicker in a nice gradual way as you trace them upwards.
An additional factor is related to the density. You can lower the density of a magma if you allow the gases in it to expand under lower pressure regimes (i.e., at shallower depths). The basaltic lava from this volcano has been previously measured to have about 2% water by weight. As this water exsolves from the magma at shallow depths (lower pressures), it will make bubbles that expand, and lower the density of the magma. However, at shallower depths, the rock surrounding the dike is under less pressure too, so they both decrease their densities in tandem.
Deviations from the expected dike geometries can be observed in some of the field measurements. For instance, in the lower-right-hand corner of Figure 3, dike “110-01” flares out to a wider thickness right as it crosses a stratum of “poorly consolidated scoriaceous tuff” within the volcano. The authors suggest that this rock type has a lower Young’s modulus. Because it’s poorly consolidated, it’s less elastic. A lower E value in equation #1 results in a larger b value, the thickness of the dike. Cool!
Now, the feeder dikes have a constant thickness all the way up. To the authors of the paper, this suggests that in the course of the eruption, these dikes reached a stress equilibrium with the surrounding host rock. Magma, being fluid, flowed away from highly-pressurized zones, and the dike thickness “evened out.” And why do the feeder dikes abruptly get wider at the top? The authors postulate a couple of possible reasons: First to consider is the elastic free-surface effect, which is essentially saying that as a dike approaches the surface of the Earth, half of the surrounding rock elasticity is lost (replaced by air), and so that control “hemming in” the dike is lost, and the dike expands. Second, erosion is probably an important factor, as the flowing magma churns away at the wall rock, breaking it down thermally as well as dynamically. In other words, some of the rock that used to be there at the edge of the fissure has been abraded or melted away as a consequence of all that lava flowing out of the dike and away over the surface.
Take home message? To quote the authors, “Feeders propagate and grow as non-feeders before they reach the surface. Therefore, the geometric difference between these types of dike… is primarily a reflection of the feeders reaching the surface.”
I’m interested in feeder dikes because Neoproterozoic feeder dikes of the Catoctin Formation are a significant piece of the geologic story of Virginia’s Shenandoah National Park:

…But these are interpreted as feeder dikes. To my knowledge, no one has claimed any particular outcrop in the Blue Ridge province as a spot where you can actually see the dike flare out and transition into a Neoproterozoic spatter cone. I picked up the Geshi, et al. paper in the first place because I wanted to know whether there was some measurable aspect of the Shenandoah dikes’ geometries that could tell me if indeed they were feeder dikes. The problem is that the exposure in Virginia (especially vertically) isn’t quite as good as the exposure on the inside of Miyakejima’s caldera. We’re lucky if we get 10 meters of vertical exposure, and there’s no suggestion from the Miyakejima data that that 10 m is sufficient to “profile” the dike sufficiently precisely to say whether it’s got a feeder geometry or not, especially if you don’t know where in the dike’s profile that 10 m vertical segment lies. So maybe all we Virginians can do is just interpret: we’ve got a bunch of Neoproterozoic dikes cutting basement rock, and atop the basement rock a bunch of Neoproterozoic lava flows, therefore some of those dikes are likely to be feeders.
_____________________________________________________
Geshi, N., Kusumoto, S., & Gudmundsson, A. (2010). Geometric difference between non-feeder and feeder dikes Geology, 38 (3), 195-198 DOI: 10.1130/G30350.1



 Callan Bentley is Associate Professor of Geology at Piedmont Virginia Community College in Charlottesville, Virginia. He is a Fellow of the Geological Society of America. For his work on this blog, the National Association of Geoscience Teachers recognized him with the James Shea Award. He has also won the Outstanding Faculty Award from the State Council on Higher Education in Virginia, and the Biggs Award for Excellence in Geoscience Teaching from the Geoscience Education Division of the Geological Society of America. In previous years, Callan served as a contributing editor at EARTH magazine, President of the Geological Society of Washington and President the Geo2YC division of NAGT.
Callan Bentley is Associate Professor of Geology at Piedmont Virginia Community College in Charlottesville, Virginia. He is a Fellow of the Geological Society of America. For his work on this blog, the National Association of Geoscience Teachers recognized him with the James Shea Award. He has also won the Outstanding Faculty Award from the State Council on Higher Education in Virginia, and the Biggs Award for Excellence in Geoscience Teaching from the Geoscience Education Division of the Geological Society of America. In previous years, Callan served as a contributing editor at EARTH magazine, President of the Geological Society of Washington and President the Geo2YC division of NAGT.
Boy oh boy, is that cinder cone/feeder dike/caldera wall complex begging to be GigaPanned!!! Wow!
Sorry, Callan, I don’t think Rick Sanchez would understand that. But thanks for this post… I saw the abstract a few days ago, and sort of set it aside (with another on geology’s roots in the Copernican Revolution) as a basis for a post on why I wish I could afford GSA dues. I never sat down and read an entire issue of Geology or GSA Bull., but almost every issue had articles that were fascinating. Again, this is one that really caught my attention, and I appreciate the information.
Your Neoproterozoic dike looks just like our Triassic-Jurassic dikes. See them at:
http://facstaff.gpc.edu/~pgore/myphotos/georgia/diabasedike1.jpg
http://facstaff.gpc.edu/~pgore/myphotos/georgia/diabasedike2.jpg LONG dike in quarry wall. Maybe someone can do the math and see if this is a feeder dike. Neat, huh?
http://facstaff.gpc.edu/~pgore/myphotos/georgia/diabasedike3.jpg
http://facstaff.gpc.edu/~pgore/myphotos/georgia/diabasedike4.jpg
…there’s something uniformitarian about that resemblance!
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] hey, how often does nature make a spectacular exposure of intrusive igneous relations on her own? (Callan found a spectacular one, but that one’s a bit farther afield than I’ve had the opportunity to venture, at least […]
[…] supercontinent Rodinia. This episode of tectonic rifting is preserved in lava flows like this, the feeder dikes which fed them, and associated pyroclastic deposits (tuffs and volcanic breccias). There are […]
[…] Shenandoah National Park, astride Virginia’s Blue Ridge, feeder dikes of Catoctin Formation (meta-)basalt cut across the Grenvillian-aged granitoid basement. Due to their mafic composition […]
[…] Shenandoah National Park, astride Virginia’s Blue Ridge, feeder dikes of Catoctin Formation (meta-)basalt cut across the Grenvillian-aged granitoid basement. Due to their mafic composition […]